2024年单招考试文化素质考试大纲
 收藏
收藏
济源职业技术学院2024年单独考试招生
文化素质考试大纲
一、考生面向
语文、数学的高中学业水平考试成绩或中职学校学业水平考试成绩均在C等级以上的考生,不再参加学校组织的文化素质考试。
二、考试形式与时间
1.考试形式:笔试。
2.总分150分,其中语文90分,数学60分。
3.考试时长:100分钟。
三、考试内容
文化素质考试范围:《中等职业学校公共基础课程教学标准》和高中教育阶段语文、数学的课程标准。具体内容如下:
(一)语文
1.考试要求
(1)识记:指识别和记忆,是最基本的能力层级。要求能识别和记忆语文基础知识、文化常识和名句名篇等。
(2)理解:指领会并能作简单的解释,是在识记基础上高一级的能力层级。要求能够领会并解释词语、句子、段落等的意思。
(3)分析综合:指分解剖析和归纳整合,是在识记和理解的基础上进一步提高了的能力层级。要求能够筛选材料中的信息,分解剖析相关现象和问题,并予以归纳整合。
(4)鉴赏评价:指对阅读材料的鉴别、赏析和评说,是以识记、理解和分析综合为基础,在阅读方面发展了的能力层级。
(5)表达应用:指对语文知识和能力的运用,能够正确判断和运用比喻、比拟、借代、夸张、对偶、排比、设问、反问等修辞手法,是以识记、理解和分析综合为基础,在表达方面发展了的能力层级。
(6)探究:指对某些问题进行探讨,有发现、有创见,是以识记、理解和分析综合为基础,在创新性思维方面发展了的能力层级。
对以上六个能力层级选择性进行不同难易程度的考查。
2.考试范围
(1)现代文阅读
阅读和鉴赏中外文学作品。了解小说、散文、诗歌、戏剧等文学体裁的基本特征和主要表现手法。阅读鉴赏文学作品,应注重价值判断和审美体验,感受形象,品味语言,领悟内涵,分析艺术表现力,理解作品反映的社会生活和情感世界,探索作品蕴涵的民族心理和人文精神。
(2)古诗文阅读
阅读浅易的古代诗文。识记常见的名句名篇;理解常见文言实词在文中的含义;理解与现代汉语不同的句式和用法;不同的句式和用法:判断句、被动句、宾语前置、成分省略和词类活用;了解并掌握常见的古代文化知识;理解并翻译文中的句子;筛选并整合文中信息;归纳内容要点,概括中心意思;分析概括作者在文中的观点态度;鉴赏文学作品的形象、语言和表达技巧;评价文章的思想内容和作者的观点态度。
(3)语言文字应用
正确、熟练、有效地使用语言文字。
(4)写作
掌握命题作文、材料作文、话题作文的基本写作方法。
(二)数学
1.命题原则
思想性:反映加强思想道德教育、民族精神教育和科学的世界观、人生观、价值观教育的要求,促进考生形成正确的情感、态度、价值观。
科学性:符合考试说明的要求,做到试卷结构合理、规范;试题内容科学、严谨,文字材料简洁、明确,参考答案合理、准确,评分标准客观、公正;试题的难度要求适当,思考量、阅读量和书写量适中,具有一定的区分度;在注重基础的同时,突出学科思想方法,关注考生的发展潜力。
基础性:重视基础知识与基本技能的考查。在考查学生对基础知识与基本技能掌握和应用程度的基础上,注重考查学生的科学探究能力,同时关注情感、态度与价值观的考查。避免出现繁、难、偏、旧试题。
2.考试要求
对考试内容的要求分为三个层次:
了解:初步知道知识的含义及其简单应用。
理解:懂得知识的概念和规律(定义、定理、法则等)以及与其他相关知识的联系。
掌握:能够应用知识的概念、定义、定理、法则去解决一些问题。
3.考试范围与内容
(1)集合
理解集合的概念、元素与集合的关系、空集。能够熟练地应用“
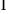 ”和“
”和“
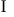 ”,熟练区分“
”,熟练区分“
 ”和“
”和“
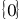 ”的不同。
”的不同。
掌握集合的表示法、常用数集的概念及其相对应的符号。能够灵活地用列举法或描述法表示具体集合;能够准确地区分“五个数集”(自然数集、正整数集、整数集、有理数集、实数集)及其符号。
掌握集合间的关系(子集、真子集、相等)。能够分清子集与真子集的联系与区别,分清集合间的三种关系和对应的符号,能准确应用集合与集合关系的符号和元素与集合关系符号。
理解集合的运算(交集、并集、补集)。能够很熟练地进行集合的交、并、补运算,对用不等式形式表示的集合运算,会用数轴帮助解决。
(2)不等式
了解不等式的基本性质。熟记不等式的三条性质,会根据不等式性质解一元一次不等式(组)。
掌握区间的基本概念。能够熟练写出九种区间所表示的集合意义和几何意义,能够直接应用区间进行集合的交、并、补运算,并能将一些问题(如,解一元二次不等式、含绝对值的不等式)的结果表示成区间形式。
掌握利用二次函数图像解一元二次不等式的方法。能够熟练地作出简单二次函数的草图,根据图像写出对应一元二次方程和一元二次不等式的解集。
了解含绝对值的一元一次不等式的解法。会解简单的含绝对值的一元一次不等式。
(3)函数
理解函数的概念。能够用集合的观点理解函数的概念,明白函数的“三要素”。会求简单函数的定义域(仅限含分母,开平方及两者综合的函数)、函数值和值域。
理解函数的单调性与奇偶性。理解函数单调性的定义,能够根据函数图像写出函数的定义域、值域、最大值、最小值和单调区间。理解函数奇偶性的定义,能根据定义和图像判断函数的奇偶性。
(4)指数函数与对数函数
了解实数指数幂;理解有理指数幂的概念及其运算法则。对根式形式和分数指数幂形式进行熟练转化。
了解幂函数的概念。会从简单函数中辨别出幂函数。
理解指数函数的概念、图像与性质。掌握指数函数的一般形式并举例,能根据图像掌握指数函数的性质(包括定义域、值域、单调性)。
理解对数的概念(含常用对数、自然对数)。能够熟练地对指数式和对数式进行互化并应用,熟记对数的性质(
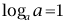 ,
,
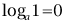 )。理解并能区别常用对数和自然对数。
)。理解并能区别常用对数和自然对数。
了解对数函数的概念、图像和性质。能举出简单的对数函数例子,会描述对数函数的图像和性质。
(5)三角函数
了解任意角的概念。能陈述正角、负角、零角的规定;对所给角能判断它是象限角还是界限角;能根据终边相同角的定义写出终边相同角的集合和规定范围内的角。
理解弧度制概念及其与角度的换算。能够快速地把角由角度换算为弧度或由弧度换算为角度(可借助计算器)。
理解任意角正弦函数、余弦函数和正切函数的概念。能结合图形理解任意角的正弦函数、余弦函数和正切函数的概念;根据概念:理解这三种函数的定义域;判别各象限角的三角函数值(正弦函
 数、余弦函数、正切函数)正负;理解并熟记界限角的三角函数值(正弦函数、余弦函数、正切函数)。
数、余弦函数、正切函数)正负;理解并熟记界限角的三角函数值(正弦函数、余弦函数、正切函数)。
理解同角三角函数的基本关系式:
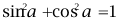 、
、
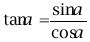 。根据三角函数概念理解这两个基本关系式,并会利用公式进行计算、化简和证明。
。根据三角函数概念理解这两个基本关系式,并会利用公式进行计算、化简和证明。
了解诱导公式:
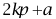 、
、
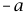 、
、
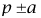 的正弦、余弦及正切公式。了解以上公式的推导过程,并会应用这三类公式进行简单计算、化简或证明。
的正弦、余弦及正切公式。了解以上公式的推导过程,并会应用这三类公式进行简单计算、化简或证明。
理解正弦函数的图像和性质。能够用“五点法”作出正弦函数的图像,并根据图像写出正弦函数的性质。
了解余弦函数的图像和性质。能根据余弦函数图像说出余弦函数的性质。
(6)数列
了解数列的概念。发现数列的变化规律,并写出通项公式。
理解等差数列的定义,通项公式,前n项和公式。会利用已知公式中的三个量求第四个量的计算。
理解等比数列的定义,通项公式,前n项和公式。会利用已知公式中的三个量求第四个量的计算。
(7)平面向量
了解平面向量的概念。利用平面中的向量(图形)分析有关概念
理解平面向量的加、减、数乘运算。会利用三角形法则、平行四边形法则和数乘运算法则进行有关运算。
了解平面向量的坐标表示。会用向量的坐标进行向量的线性运算、判断向量是否共性。
了解平面向量的内积。理解用坐标表示内积、用坐标表示向量垂直关系。
(8)直线和圆的方程
掌握两点间距离公式及中点公式。
理解直线的倾斜角与斜率。利用斜率公式进行倾斜角和斜率的计算。
掌握直线的点斜式方程和斜截式方程。灵活应用两种方程进行直线的有关计算。
理解直线的一般式方程。理解几种形式方程的相互转化,由一般式方程求直线的斜率。
掌握两条相交直线交点的求法。会判断两条直线的位置关系,求相交直线的交点坐标
理解两条直线平行的条件。会求过一点且与已知直线平行的直线方程。
理解两条直线垂直的条件。会求过一点且与已知直线垂直的直线方程。
了解点到直线的距离公式。会用公式求点到直线的距离。
掌握圆的标准方程和一般方程。由圆的标准方程和一般方程求圆的圆心坐标和半径,会根据已知条件求圆的方程。
理解直线与圆的位置关系。会用圆心到直线的距离与半径的关系判断直线与圆的位置关系。
















